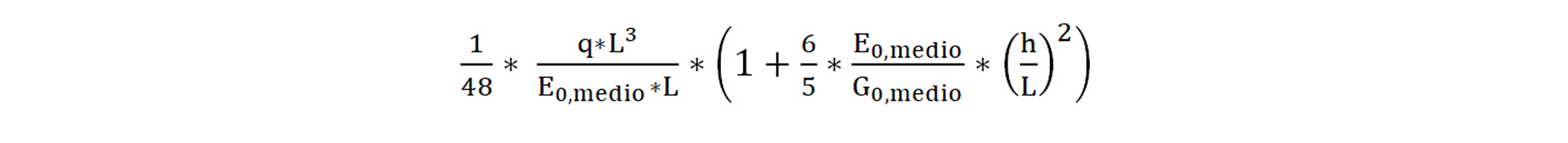En esta publicación teórica vamos a conocer los parámetros que necesitamos para calcular nuestro forjado.
La normativa que utilizaremos es la siguiente:
CTE-DB-SE. Seguridad Estructural.
CTE-DB-SE-AE. Acciones en la edificación.
CTE-DB-SE-M. Estructuras de Madera.
CTE-DB-SI. Seguridad frente a incendio.
UNE EN 1995-1-1/AN:2016-04. Parte 1-1.
UNE EN 1995-1-2. Parte 1-2.
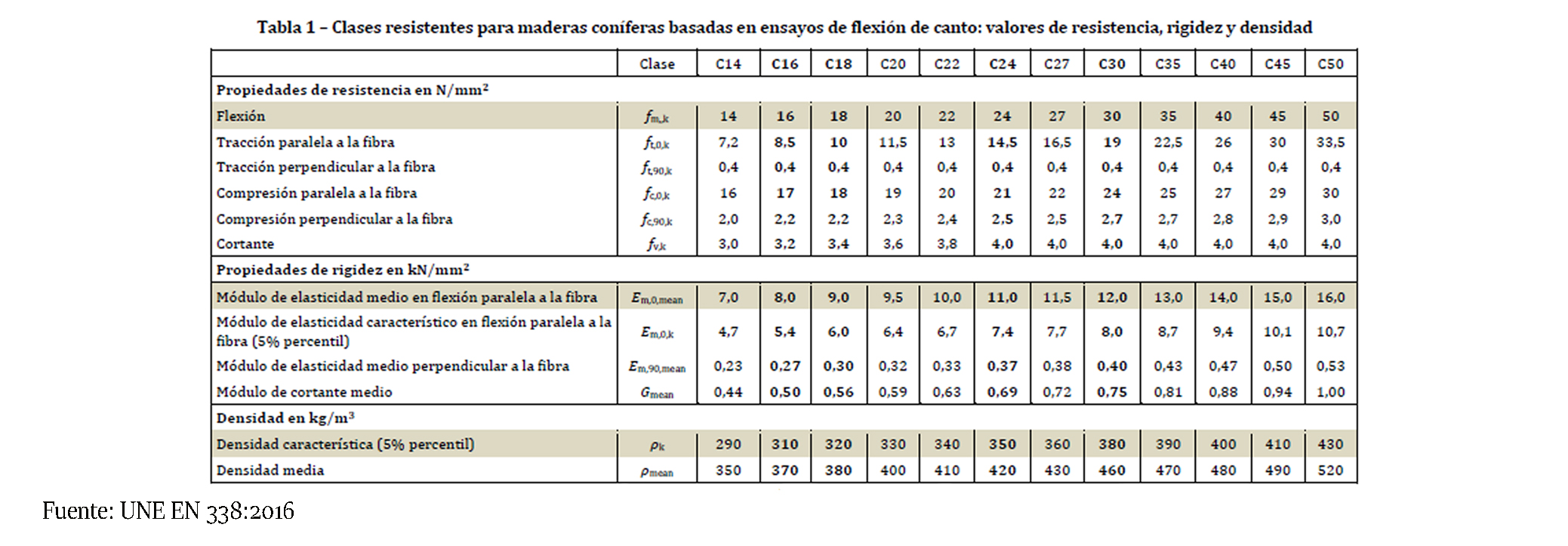
UNE EN 338:2010. Madera estructural. Clases resistentes.
PARTE I
Esta publicación es meramente orientativa, cada proyecto estructural es una caso particular, con unas características y condiciones específicas, que quizás no se tengan en cuenta en este artículo. Por ello, podemos usar esta información como guía de cálculo, para hacernos a la idea de las magnitudes de nuestra estructuras. En caso de querer tener un cálculo fiable con nuestra realidad debemos recurrir a la supervisión de un profesional competente en este campo.
¿CÓMO ES NUESTRA ESTRUCTURA?
PARÁMETROS GEOMÉTRICOS
Un forjado es un elemento estructural horizontal (0º) o inclinado (cubiertas xº), constituido por vigas y viguetas, las cuales tienen un ancho b (mm), un canto h (mm) y una longitud L (m). Además, para el cálculo de estructuras es necesario conocer el ancho tributario*, s (m), que existe entre las viguetas que forman nuestro forjado.
*Ancho tributario: es la banda de carga que un elemento estructural asume.
PARÁMETROS DE LA MADERA
Conocer con qué tipo de madera, y dónde vamos a trabajar es muy importante, ya que determinará otros parámetros del cálculo. La madera estructural se clasifica según tres conceptos:
–Producto primario: Madera Aserrada (MA), Madera Laminada Encolada (MLE) y Madera Microlaminada (LVL).
–Clase resistente: maderas coníferas (C), maderas frondosas (D), madera laminada homogénea (GLh) o madera laminada combinada GLc.
–Clase de servicio: CS1,CS2 y CS3.
ACCIONES EN LA EDIFICACIÓN
Es imprescindible conocer las acciones que actúan sobre nuestras estructuras, para poder verificar el cumplimiento de los requisitos de seguridad estructural (capacidad portante y estabilidad) y aptitud al servicio.
Acciones permanentes G (kN/m)
Son la suma de las cargas del peso propio (elementos estructurales, cerramiento, tabiquería, rellenos, equipos fijos..), así como de las acciones del terreno.
Acciones variables
Carga uso puntual P (kN) *
Carga uso uniforme Q (kN/m) *
Carga nieve qn (kN/m)
Carga viento 0º Tipo 1 qv1 (kN/m)
Carga viento 0º Tipo 2 qv2 (kN/m)
Carga viento 90º qv (kN/m)
*Las acciones de uso dependen de la categoría de uso:
Categoría A. Zonas residenciales.
Categoría B. Zonas administrativas.
Categoría C. Zonas destinadas al público.
Categoría D. Zonas comerciales.
Categoría E. Zonas de tráfico y aparcamiento.
Categoría F. Cubiertas transitadas accesibles sólo privadamente.
Categoría G. Cubiertas de mantenimiento.
 Resistencia a flexión
Resistencia a flexión 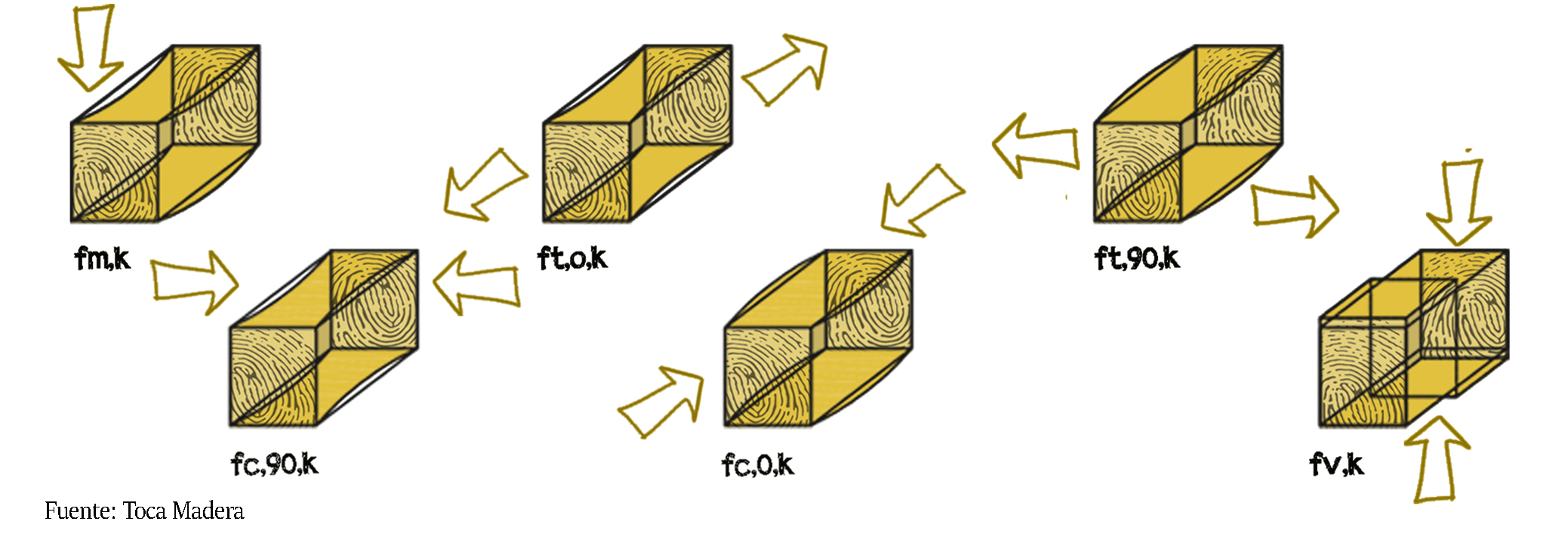

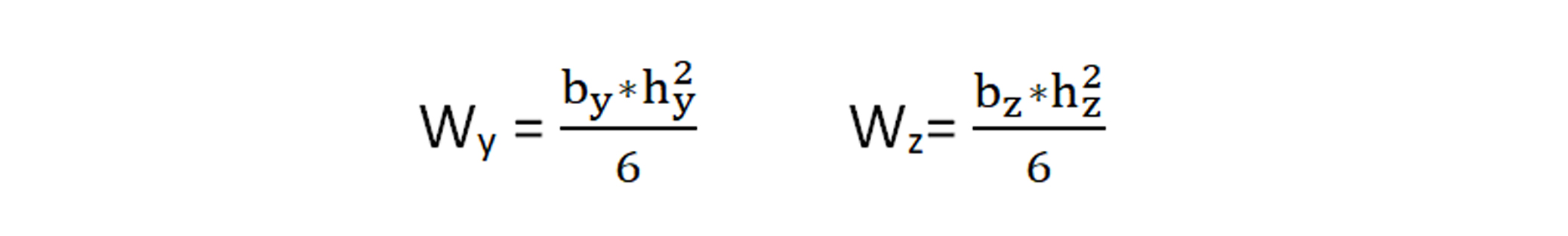 El
El 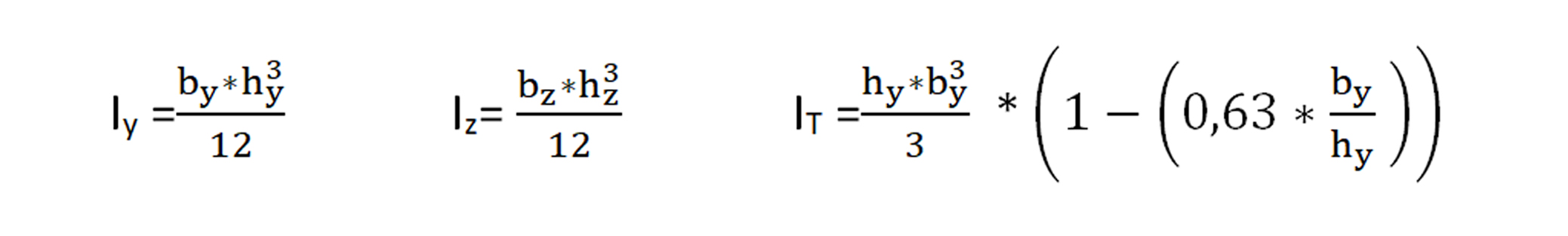
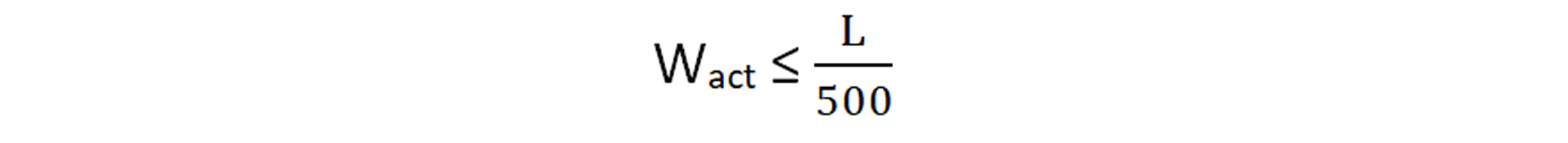 Forjados y cubiertas con tabiques o pavimentos frágiles.
Forjados y cubiertas con tabiques o pavimentos frágiles.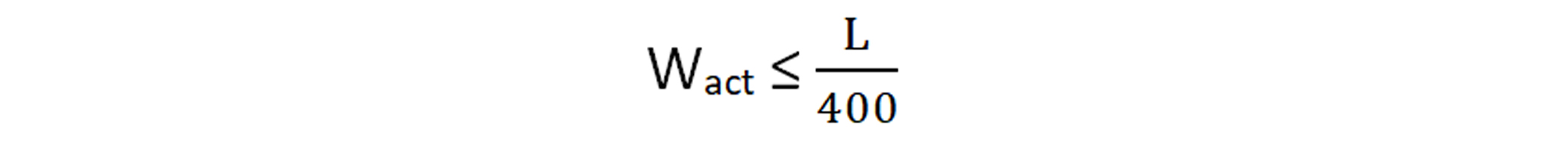 Forjados y cubiertas con tabiques o pavimentos ordinarios.
Forjados y cubiertas con tabiques o pavimentos ordinarios.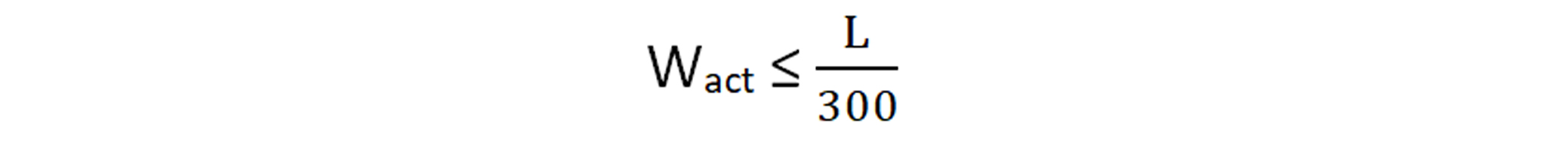 Resto de los casos
Resto de los casos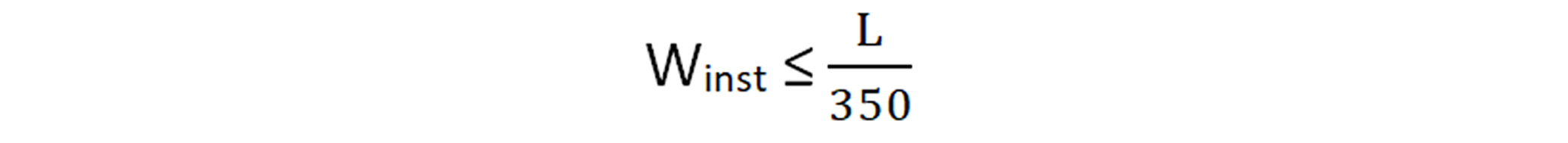
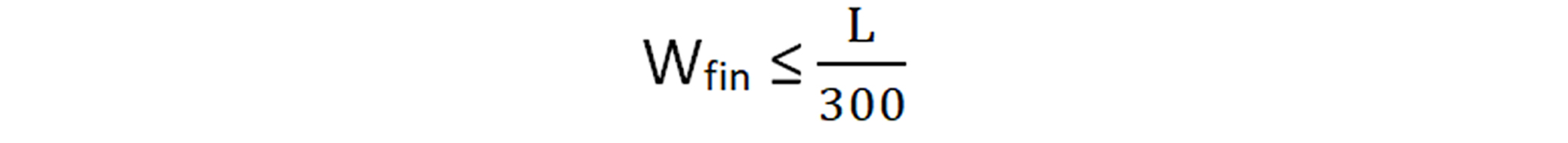 La flecha es el descenso del vano, producido por una flexión, respecto a su posición inicial.
La flecha es el descenso del vano, producido por una flexión, respecto a su posición inicial.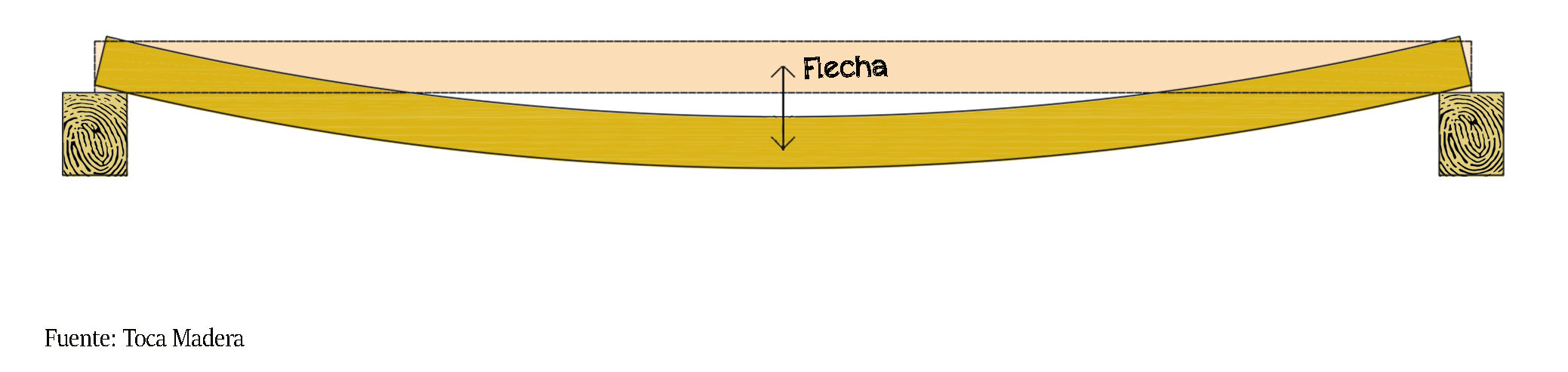 Flecha de carga uniforme
Flecha de carga uniforme 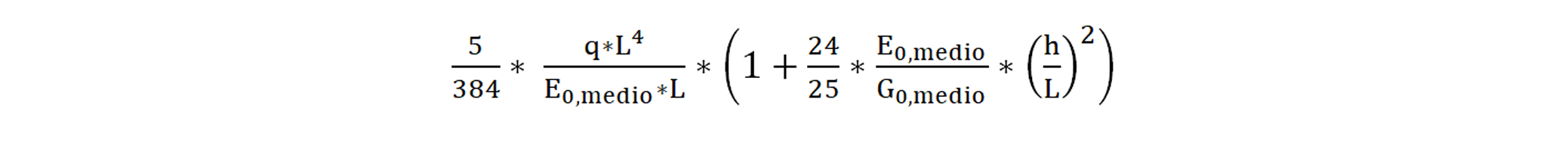 Flecha de carga puntual
Flecha de carga puntual