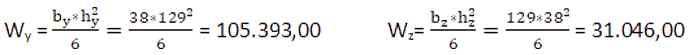Con esta publicación finalizamos el cálculo práctico de un forjado de madera a fuego, viento y nieve. Continuación de la Parte I .
En los siguientes enlaces podéis repasar los temas teóricos de iniciación al cálculo de estructuras de madera.
Parte I
Fuego
Parte II
PARTE II.
Esta publicación es meramente orientativa, cada proyecto estructural es una caso particular, con unas características y condiciones específicas, que quizás no se tengan en cuenta en este artículo. Por ello, podemos usar esta información como guía de cálculo, para hacernos a la idea de las magnitudes de nuestra estructuras. En caso de querer tener un cálculo fiable con nuestra realidad debemos recurrir a la supervisión de un profesional competente en este campo.
¿CÓMO ES NUESTRO PROYECTO?
Ahora, además de conocer los parámetros de la anterior publicación, sabemos su ubicación territorial y su protección frente al fuego.
ACCIONES EN LA EDIFICACIÓN
Acciones permanentes. Duración de carga permanente. G (kN/m2) = bv * hv * Pmedia + G1 * s = 0,68.
Acciones variables.
Carga uso puntual. Duración de carga corta. P (kN) = P2 = 2
Carga uso uniforme. Duración de carga media. Q (kN/m2) = Q3 * s = 0,80.
PARTE II. Nuevas acciones en la edificación : nieve y viento.
Carga nieve. Duración de carga corta. Qn (kN/m) = qn * s = 0,57 * 0,40 = 0,23.
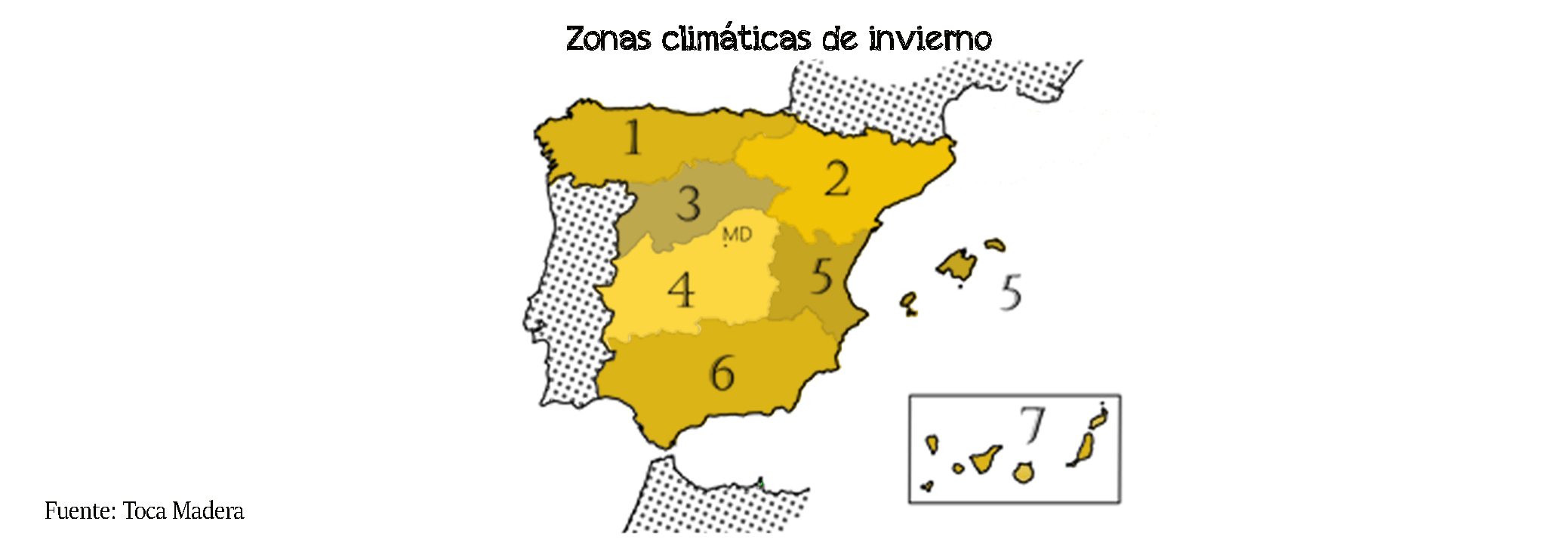
Teniendo en cuenta que es un forjado de un edificio con cubierta plana en Madrid, altitud = 657 m < 1000 m , podríamos considerar 1 kN/m2 de carga de nieve. Sin embargo, el cálculo de este caso según su altitud, su zona climática de invierno y su inclinación de la cubierta.
Según el CTE-AE, para esta altitud (657 m) y esta zona climática de invierno (4), la sobrecarga de nieve en proyección horizontal (sk) = 0,57 kN/m2
En una cubierta plana (0º) el coeficiente de forma de la cubierta (μ) =1
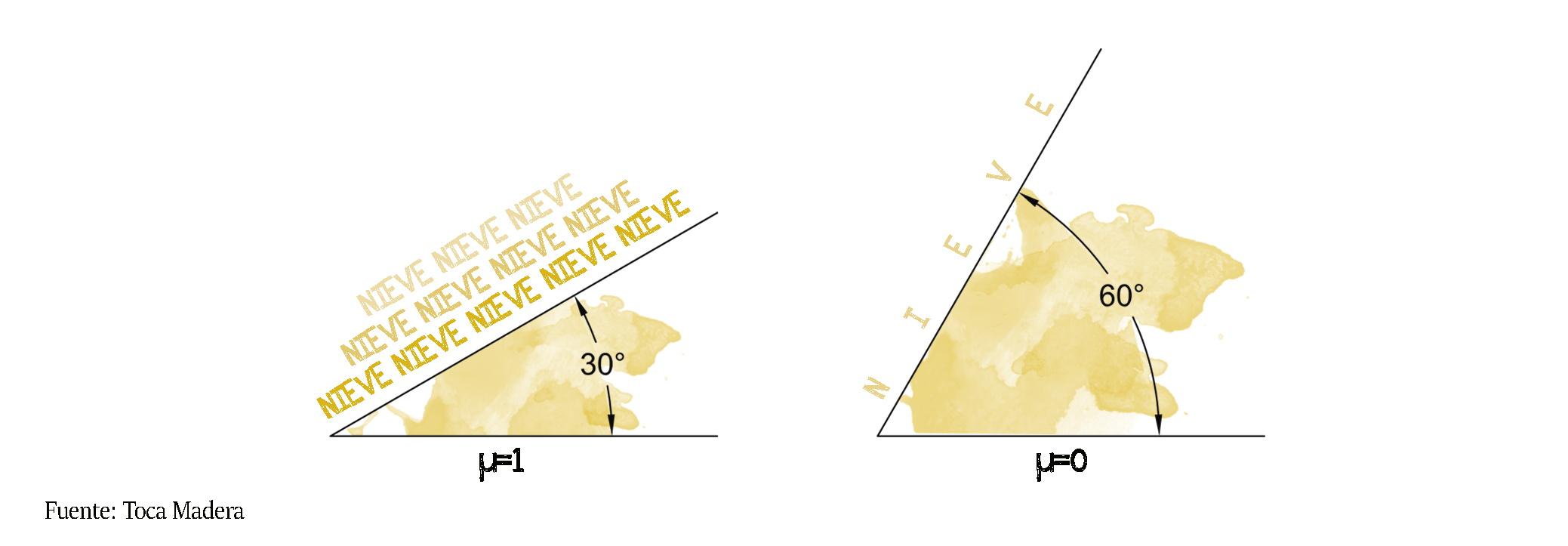
qn (kN/m2) = μ * sk = 1 * 0,57 = 0,57
Carga viento. Duración de carga corta. Para el cálculo del viento se tienen en cuenta dos direcciones, y una de ellas en sentidos opuestos.
0º Tipo 1 Qv1 (kN/m) = qv1 * s = 0,42 *1,7 *+0,2* 0,4 = 0,06
0º Tipo 2 Qv2 (kN/m) = qv2 * s = 0,42 *1,7 *-0,7 * 0,4 = 0,20
90º Qv (kN/m) = qv * s = 0,42 *1,7 *-1,2 * 0,4 = -0,34
La edificación de planta rectangular, se sitúa en una zona urbana de la ciudad de Madrid. Considerando estos factores se determinan los siguientes parámetros.
La presión dinámica del viento (qb) se establece en función de la zona de la velocidad básica a la que pertenezca Madrid (A) : 0,42 kN/m2

El coeficiente de exposición (Ce), depende del entorno (zona urbana -> IV) : 1,7
El coeficiente de forma (Cp) depende de las dimensiones de la edificación ( largo, ancho, alto, área en planta y altura de peto), así como de la inclinación de su cubierta. Para este caso práctico la inclinación de la cubierta es 0º, su área > 10 m2, las dimensiones de la planta 20 x 10 m y la altura de la edificación 8 m y del peto 1,30 m. Siendo los coeficientes de forma (Cp) = -1,2 y -0,8 en el lado largo de la planta; y -0,7 y +0,2 en el ancho de la misma. El signo (-) de estos coeficientes indica el empuje del viento, y el (+) la posible succión de la cubierta, por ello calcularemos nuestro proyectos con los vientos más desfavorables en casa dirección, es decir, -1,2 en sentido longitudinal y -0,7 y +0,2 en su anchura.
qv= qb * Ce * Cp (kN/m2)
Las acciones de uso dependen de la categoría de uso:
Categoría G. Cubiertas solo mantenimiento
Las combinaciones de acciones posibles son:
A. 1,35 * G
B. 1,35 * G + 1,50 * P
C. 1,35 * G + 1,50 * Q
D. 1,35 * G + 1,50 * Qn
E. 1,35 * G + 1,50 * Qv1
F. 1,35 * G + 1,50 * Qv2
G. 1,35 * G + 1,50 * Qv
H. 1,35 * G + 1,50 * Qn + 0,90 * Qv1 -> 0,90 = 1,50 * Ψ0,viento
I. 1,35 * G + 1,50 * Qn + 0,90 * Qv2 -> 0,90 = 1,50 * Ψ0,viento
J. 1,35 * G + 1,50 * Qn + 0,90 * Qv -> 0,90 = 1,50 * Ψ0,viento
K. 1,35 * G + 0,75 * Qn + 1,50 * Qv1 -> 0,75 = 1,50 * Ψ0,nieve
L. 1,35 * G + 0,75 * Qn + 1,50 * Qv2 -> 0,75 = 1,50 * Ψ0,nieve
M. 1,35 * G + 0,75 * Qn + 1,50 * Qv -> 0,75 = 1,50 * Ψ0,nieve
N. 0,80 * G + 1,50 * Qv1
O. 0,80 * G + 1,50 * Qv2
P. 0,80 * G + 1,50 * Qv
Para saber qué caso es el más desfavorable en cada situación, debemos calcular todas las combinaciones y quedarnos con la de mayor resultado. Sin embargo, en este ejercicio ya sabemos cuál es la peor, se mantienes las mismas combinaciones que en la Parte I del ejercicio, las acciones de nieve y viento no suponen grandes cargas.
FUEGO
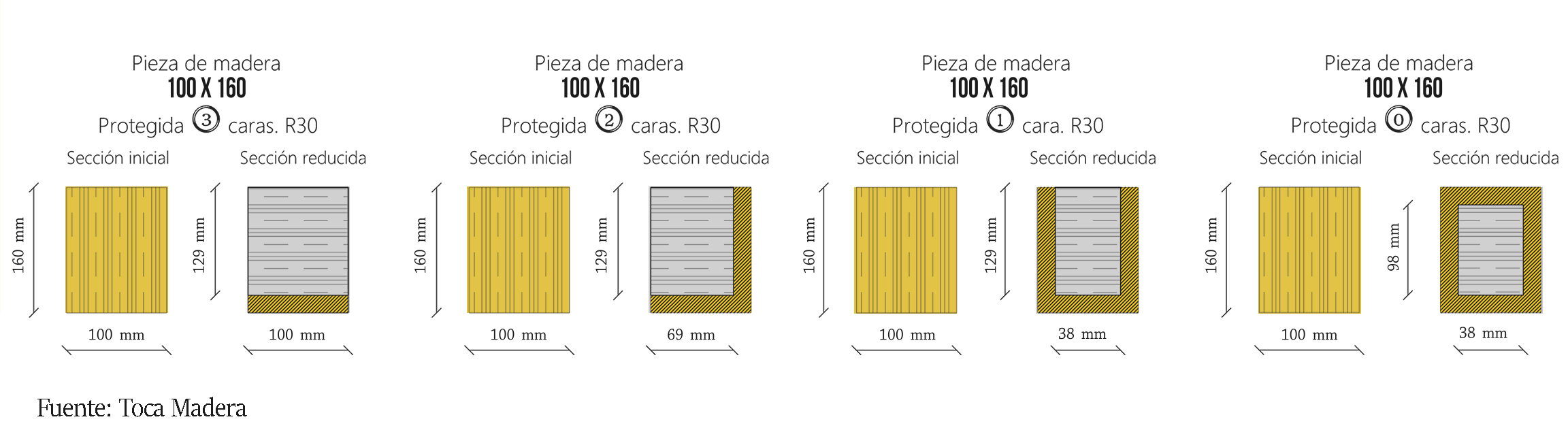
El problema que presentan las piezas de madera tras un incendio, no es tanto de pérdida de resistencia, sino de reducción de su sección. Para conocer si las piezas de este ejercicio mantienen su capacidad resistente tras el fuego, primero debemos conocer la sección resultante del elemento.
La carbonización nominal de cálculo, según el CTE-DB-SI, para una madera C24, conífera con pk > 290kg/m3, en un tiempo de 30 minutos:
dchar,n (mm) = t * βn = 30 * 0,80 = 24
La profundidad eficaz de carbonización determina la sección perdida durante el incendio, siendo do (7) y ko (1) para superficies no protegidas durante más de 20 minutos.
def (mm) = dchar,n + d0 * k0 = 24 + 7 * 1 = 31
PARÁMETROS GEOMÉTRICOS
Conociendo la profundidad eficaz de carbonización, y teniendo en cuenta que las viguetas sólo están protegidas por la parte superior, se determinan los parámetros geométricos a fuego.
º = 0 bv = 100 – (31*2) = 38 mm hv = 160 – 31 = 129 mm Lv = 3,50 m s = 0,40 m
– Factor de carga compartida. Ksys = 1,1
– Factor de la sección. KM = 0,70
– Factor de altura. Kh = 1,03
PARÁMETROS DE LA MADERA.
Madera aserrada de coníferas, C24.
– Factor de cortante. Kcr = 0,67
– Coeficiente de seguridad del material. ϒM‘ = 1,00
Clase de servicio 1.
– Factor de modificación. Kmod siempre en fuego = 1
– Factor de fluencia. Kdef = 0,60
CÁLCULO.
CARACTERÍSTICAS GEOMÉTRICAS DE LA SECCIÓN
Módulo resistente (mm3)
Momento de inercia (mm4)
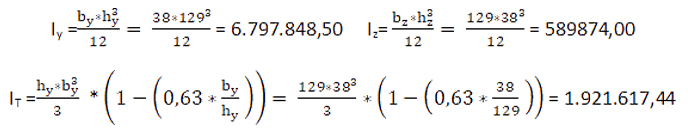
ESTADOS LÍMITES.
ESTADO LÍMITE ÚLTIMO
Las acciones de uso dependen de la categoría de uso:
Categoría G. Cubiertas solo mantenimiento.